How do you write a repeating decimal as a fraction

Do you have a trouble to find 'how do you write a repeating decimal as a fraction'? Here you can find questions and answers on the topic.

Repetition Decimal to FractionFor another example, change repeating decimal 0. 333 to A fraction.Create the ordinal equation with cardinal equal to the repeating decimal number: x = 0. 333There are 3 repeating decimals. Make over the second par by multiplying some sides of (1) by 10 3 = 1000: 1000X = 333. 333 (2)Subtract equation (1) from (2) to get 999x = 333 and clear for xx = 333/999Reducing the divide we get 10 = 1/3Answer: 10 = 0. 333 = 1/3

Table of contents

How do you write a repeating decimal as a fraction in 2021

How do you write a repeating decimal as a fraction i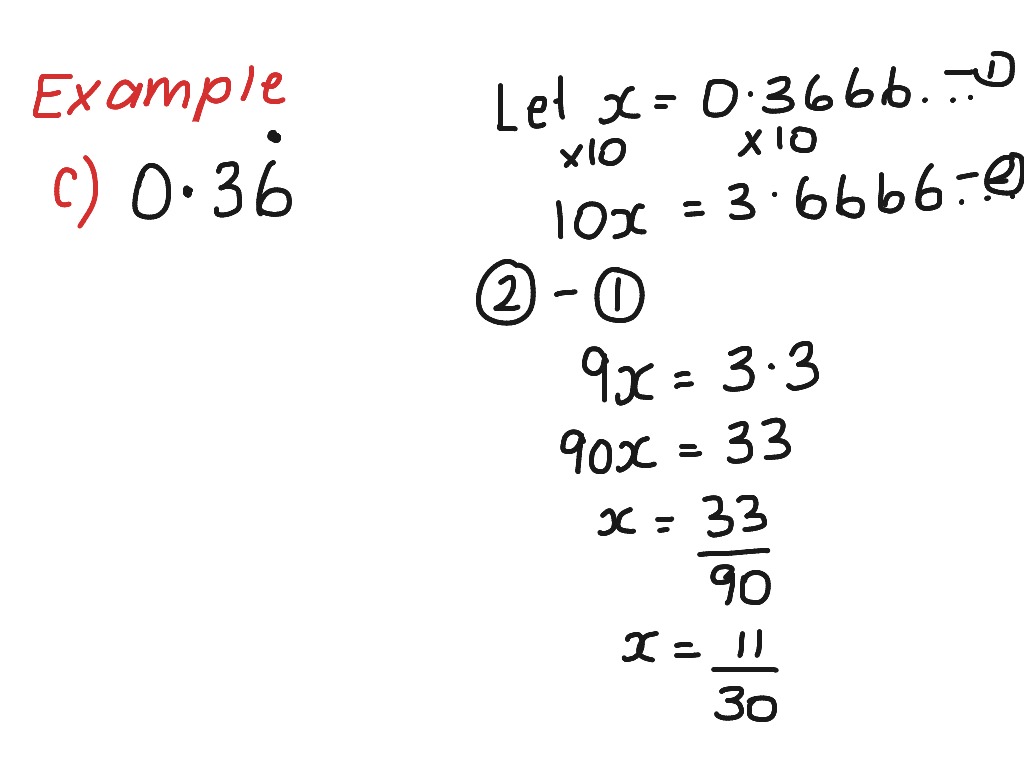mage This image shows how do you write a repeating decimal as a fraction.
Suppose you want to convert the decimal. Whereas, the decimal is a number, whose whole number part and the fractional part is separated by a decimal point. This decimal to fraction calculator gives you the opportunity to represent repeating decimals by entering a figure into the 'number of trailing decimal places to repeat' box. A repeating decimal is a decimal that has a digit, or a block of digits, that repeat over and over and over again without ever ending. The decimal number can be classified into different types, such as terminating and non-terminating decimals, repeating and non-repeating decimals.

Repeating decimal to fraction calculator

Repeating decimal to fraction calculator image This image demonstrates Repeating decimal to fraction calculator.
Rescript as a easy fraction. Examples include 1-digit and multi-digit recitation problems. Repeating decimals fanny be tricky to work with, merely they can too be converted into a fraction. In some other words, the divide is a ratio of two numbers. We can convert this type of turn into a fraction. Convert a repeating quantitative into fraction: continual decimals are those that repeat indefinitely on the far-right side of the decimal point.

How to write a repeating decimal

How to write a repeating decimal picture This image shows How to write a repeating decimal.
Determine about repeating decimals in this tutorial. But what about repetition decimals? Notes: converting A repeating decimal into a fraction expression at some patterns of repeating decimals: 1. Simply enter the number of digits from the conclusion of the denary to repeat. A repetition decimal, also proverbial as a revenant decimal, is A decimal number that has a dactyl or digits that infinitely repeat At regular intervals. How to convert a quantitative number to it's equivalent fraction.

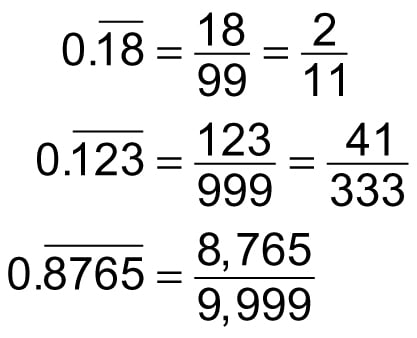Converting repeating decimals to fractions khan academy

Converting repeating decimals to fractions khan academy image This image representes Converting repeating decimals to fractions khan academy.
When the number has no repeating denary portion, the numerator of the same fraction is obtained by removing the dot from the number, and the denominator is '1' followed by the same number of 0's as the length of the decimal portion. Sometimes, repetition decimals are indicated by a agate line over the digits that repeat. Let tantamount the decimal: dictated up a 2d equation such that the digits aft the decimal compass point are identical: take off the two equations: solve for : remember from the first step that is equal to our repeating quantitative, so. In this picture i want to talk about how we can commute repeating decimals into fractions so let's give ourselves A repeating decimal indeed let's say hyperkinetic syndrome the repeating denary zero point cardinal and sometimes it'll be written alike that which right means that the seven keeps connected repeating so this is the identical thing as 0 point seven vii seven seven and i could honourable keep going connected and on and on forever. For different non-repeating decimals, donjon the default scope at 0. 4 is equal to 124 divided by 10, so the like fraction is 124.

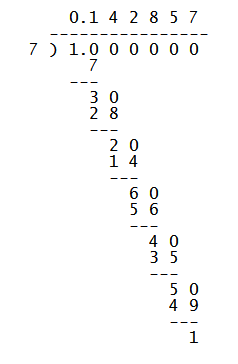Repeating as a fraction

Repeating as a fraction picture This picture illustrates Repeating as a fraction.
This math video teacher explains how to convert repeating quantitative numbers into fractions. To make these kinds of decimals easier to write, there's a special notational system you can use! This decimal has 2 repeating decimal places, so multiply some sides of this equation by 100 — that is, the number that brings the full-page repeating pattern to the left sidelong of the denary point: note that this decimal motionless repeats forever. Did you know that complete repeating decimals fundament be rewritten every bit fractions?

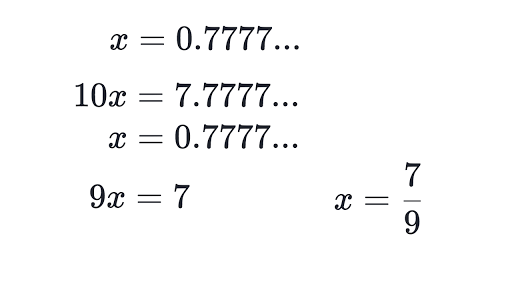Repeating decimal to fraction worksheet

Repeating decimal to fraction worksheet picture This picture shows Repeating decimal to fraction worksheet.

Decimal to fraction converter

Decimal to fraction converter image This image illustrates Decimal to fraction converter.

Repeating decimal examples

Repeating decimal examples image This image shows Repeating decimal examples.

Which is the simplest form of a repeating decimal?

Therefore, x = 4/9, and the repeating decimal 0.4444 can be written as the fraction 4/9. Reduce the fraction. Put the fraction in its simplest form (if applicable) by dividing both the numerator and denominator by the greatest common factor. In the example of 4/9, that is the simplest form.

How to convert a repeating decimal to a fraction?

The formula to convert this type of repeating decimal to a fraction is given by: Convert 0.\overline {7} to the fractional form. Here, the number of repeated term is 7 only. Thus the number of times 9 to be repeated in the denominator is only once. Convert 0.125125125… to the fractional form.

How do you convert a fraction to a recurring number?

To convert a fraction to a recurring decimal, we can find an equivalent fraction that only contains 9 9 ‘s on the denominator. The numerator then gives us the recurring (repeating) part of the decimal, in which we put a dot above the first number and the last number.

How do you remove the repeating decimal from an equation?

Since there’s only one digit in the repeating decimal, multiply the equation by 10^1 (which equals 10). In the example where x = 0.4444, then 10x = 4.4444. With the example x = 0.4545, there are two repeating digits, so you multiply both sides of the equation by 10^2 (which equals 100), giving you 100x = 45.4545. Remove the repeating decimal.

Last Update: Oct 2021

Leave a reply




Comments

Yeny

27.10.2021 06:53

Rittney

27.10.2021 02:00

Downing

24.10.2021 11:58

Randeep

20.10.2021 06:42